🔹 1. What is a Square?
- When a number is multiplied by itself, the product is called a square number or perfect square.
👉 Example:- ( 22 = 4 )
- ( 32 = 9 )
- ( 52 = 25 )
✅ General Form:
If ( a ) is any number, then
a2 = a X a
🔹 2. Properties of Square Numbers
- The square of an even number is even.
- Example: ( (4)2 = 16 )
- The square of an odd number is odd.
- Example: ( (3)2 = 9 )
- The number of zeros at the end of a perfect square is always even.
- Example: ( (20)2 = 400 ) → 2 zeros
- The square of a number ending in 2, 3, 7, or 8 never ends with 2, 3, 7, or 8.
- The square of a number ending in 1, 4, 5, 6, or 9 always ends in 1, 4, 5, 6, or 9 respectively.
- Squares of natural numbers are always positive.
- Sum of first ( n ) odd numbers = ( n2 )
1 + 3 + 5 + 7 +………….+ (2n – 1) = n2
👉 Example: ( 1 + 3 + 5 + 7 + 9 = 25 = 5^2 )
🔹 3. Perfect Squares between 1 and 100
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
👉 Total perfect squares from 1–100 = 10
🔹 4. Patterns Related to Squares
- ( 12 = 1 )
- ( 22 – 12 = 3 )
- ( 32 – 22 = 5 )
- ( 42 – 32 = 7 )
✅ Difference of consecutive squares = consecutive odd numbers
🔹 5. What is a Square Root?
The square root of a number is the value which, when multiplied by itself, gives the original number.
sqrt{a2} = a
👉 Example:
- √9 = 3
- √49 = 7
✅ Symbol: √
🔹 6. Properties of Square Roots
1️⃣ √(a × b) = √a × √b
2️⃣ √(a ÷ b) = √a ÷ √b (b ≠ 0)
3️⃣ √(a²) = a
4️⃣ (√a)² = a
✅ A perfect square always has an integer square root.
🔹 7. Methods to Find Square Roots
🟢 (A) By Repeated Subtraction Method
- The sum of the first n odd numbers = ( n2 ).
- Subtract consecutive odd numbers from the given number until you reach 0.
- The number of subtractions = square root.
👉 Example: Find √49
49 − 1 = 48
48 − 3 = 45
45 − 5 = 40
40 − 7 = 33
33 − 9 = 24
24 − 11 = 13
13 − 13 = 0
✅ Number of steps = 7 → √49 = 7
🟢 (B) By Prime Factorization Method
- Step 1: Find prime factors of the given number.
- Step 2: Make pairs of equal factors.
- Step 3: Take one factor from each pair.
- Step 4: Multiply them together.
👉 Example: Find √144
144 = 2 × 2 × 2 × 2 × 3 × 3
= (2 × 2) × (2 × 2) × (3 × 3)
√144 = 2 × 2 × 3 = 12
✅ √144 = 12
🟢 (C) By Long Division Method
Used for large numbers that are not easy to factorize.
Steps:
- Group digits in pairs from right to left (for whole number part).
- Find the largest number whose square ≤ first group.
- Subtract and bring down the next pair.
- Double the quotient and find a suitable digit ‘x’ such that
(20×quotient + x) × x ≤ dividend - Repeat the process till required decimal places.
👉 Example: Find √529
Step 1: Group digits → (5)(29)
Step 2: 2² = 4 (≤5) → remainder 1
Step 3: Bring down 29 → 129
Step 4: Double quotient = 2×2 = 4 → Try 43×3 = 129
✅ √529 = 23
🟢 (D) By Estimation Method
Used for non-perfect squares.
Steps:
- Find the two nearest perfect squares between which the number lies.
- Estimate a value between their roots.
- Refine the value by approximation.
👉 Example: √50
49 < 50 < 64
√49 = 7, √64 = 8
So √50 ≈ 7.07 (closer to 7)
🔹 8. Squares of Fractions and Decimals
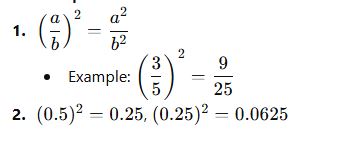
🔹 9. Square Roots of Fractions and Decimals
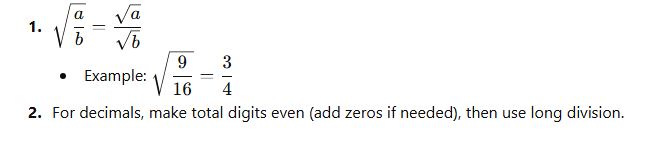
🔹 10. Estimating Square Roots (for Non-Perfect Squares)
| Number | Approx. Square Root |
|---|---|
| 2 | 1.414 |
| 3 | 1.732 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.645 |
| 8 | 2.828 |
| 10 | 3.162 |
🔹 11. Important Formulas
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b)(a – b) = a2 – b2
👉 Use these to find squares quickly.
🔹 12. Tricks to Find Squares Easily
| Type | Example | Trick |
|---|---|---|
| Ending with 5 | 25² | (2×3)=6 → 625 |
| Near 50 | 47² | 25 + (47−50)² − 3×100 + 9 = 2209 |
| Using formula | 38² | (40−2)² = 1600 − 160 + 4 = 1444 |
🔹 13. Application in Real Life
- Area of a square: A = (side)2
- Finding side from area: side = √A
- Used in geometry, physics, statistics (standard deviation), etc.
🔹 14. Practice Questions
- Find √729 by prime factorization.
- Find √225 by long division.
- Which of these are perfect squares? 400, 625, 900, 9801
- Find the smallest number to be multiplied by 180 to make it a perfect square.
- Estimate √15 up to 2 decimal places.
























Leave a comment