---

द्विघात समीकरण

1. द्विघात समीकरण क्या है ?

• जिस समीकरण में एक चर हो और उस चर की अधिकतम घात 2 हो, उसे द्विघात समीकरण कहते हैं।
• “Quadratic” शब्द लैटिन भाषा के Quadratus से लिया गया है, जिसका अर्थ वर्ग होता है।
• द्विघात समीकरणों का उपयोग गणित, भौतिकी, ज्यामिति और दैनिक जीवन की समस्याओं में होता है।

---

2. द्विघात समीकरण का मानक रूप

• किसी द्विघात समीकरण का मानक रूप होता है:

ax² + bx + c = 0

जहाँ—

• a, b, c वास्तविक संख्याएँ हैं
• a ≠ 0 होना आवश्यक है
• यदि a = 0 हो, तो समीकरण रेखीय (Linear) हो जाएगा, द्विघात नहीं

---

3. द्विघात समीकरण के उदाहरण

• x² + 7x + 10 = 0
• 2x² − 5x − 3 = 0
• x² − 9 = 0
• (x − 4)(x + 1) = 0

द्विघात नहीं हैं

• 5x + 2 = 0
• x³ − x + 1 = 0

---

4. द्विघात समीकरण के मूल (Roots)

• द्विघात समीकरण के हल को उसके मूल (Roots) कहते हैं।
• मूल वे मान हैं जिनके लिए समीकरण संतुष्ट होता है।
• एक द्विघात समीकरण के अधिकतम दो मूल हो सकते हैं।

---

5. द्विघात समीकरण हल करने की विधियाँ (NCERT)

NCERT के अनुसार द्विघात समीकरण हल करने की तीन विधियाँ हैं:

---

(A) गुणनखंड विधि (Factorisation Method)

• समीकरण को दो रैखिक गुणनखंडों के गुणनफल के रूप में लिखा जाता है।
• प्रत्येक गुणनखंड को शून्य के बराबर रखकर हल निकाला जाता है।

चरण:

1. समीकरण को मानक रूप में लिखें
2. मध्य पद का गुणनखंड करें
3. प्रत्येक गुणनखंड को शून्य के बराबर रखें
4. x के मान ज्ञात करें

---

(B) पूर्ण वर्ग विधि (Completing the Square Method)

• समीकरण को पूर्ण वर्ग के रूप में बदला जाता है।
• तब उपयोगी जब गुणनखंड संभव न हो।

चरण:

1. यदि x² का गुणांक 1 न हो, तो उससे भाग दें
2. स्थिर पद को RHS में ले जाएँ
3. x के गुणांक के आधे का वर्ग दोनों पक्षों में जोड़ें
4. प्राप्त समीकरण हल करें

---

(C) द्विघात सूत्र विधि (Quadratic Formula Method)

• यह सर्वाधिक सामान्य विधि है।
• किसी भी द्विघात समीकरण के लिए प्रयुक्त की जा सकती है।

द्विघात सूत्र:

---

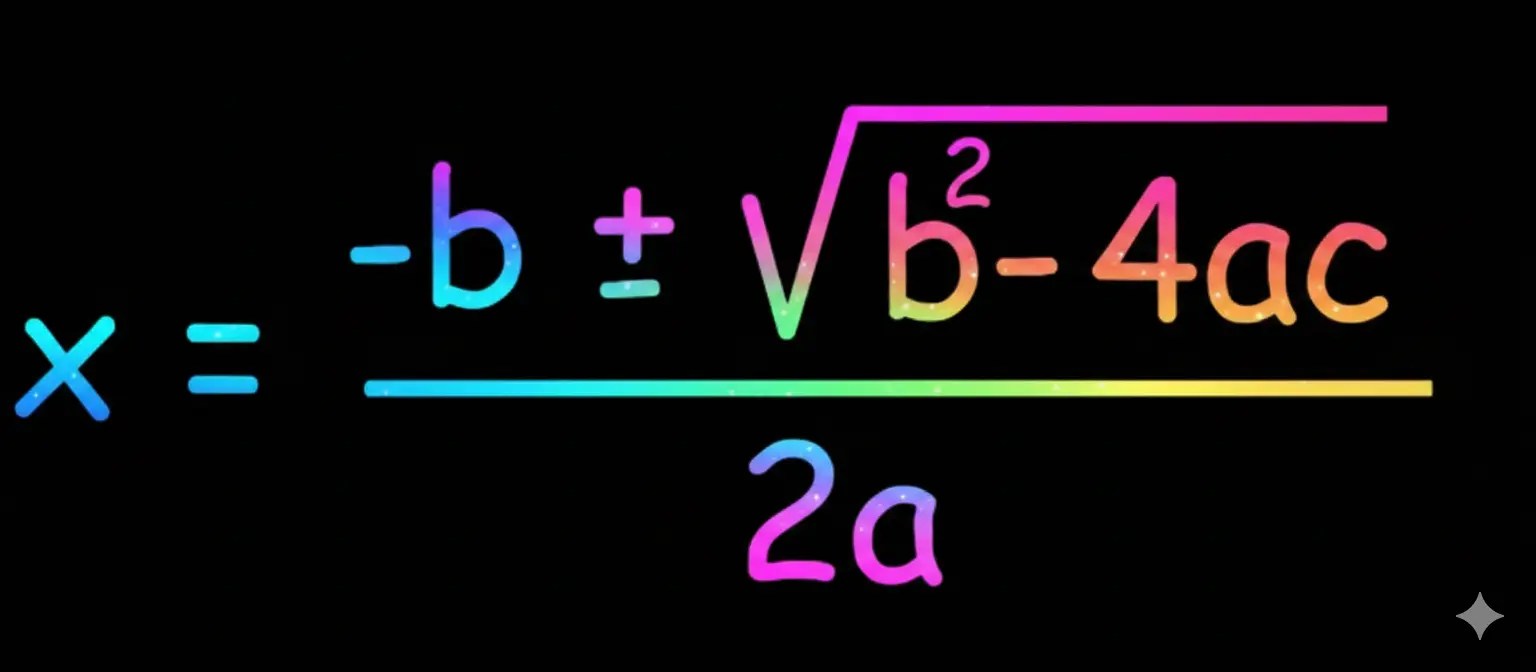
6. विविक्तकर (Discriminant)

• व्यंजक b² − 4ac को विविक्तक कहते हैं।
• इसे D से दर्शाते हैं।

D = b² – 4ac

---

7. विविक्तकर के आधार पर मूलों की प्रकृति(Nature of roots)

विविक्तक (D)	मूलों की प्रकृति
D > 0	दो भिन्न वास्तविक मूल
D = 0	दो समान वास्तविक मूल
D < 0	कोई वास्तविक मूल नहीं

---

8. द्विघात समीकरण का ज्यामितीय अर्थ

• द्विघात समीकरण का ग्राफ परवलय (Parabola) होता है।
• मूल वे बिंदु हैं जहाँ परवलय x-अक्ष को काटता या स्पर्श करता है।
  • दो बिंदुओं पर काटे → दो वास्तविक मूल
  • एक बिंदु पर स्पर्श करे → समान मूल
  • x-अक्ष को न काटे → कोई वास्तविक मूल नहीं

---

9. द्विघात समीकरण का हल

• किसी द्विघात समीकरण के:
  • दो वास्तविक हल हो सकते हैं
  • एक वास्तविक हल (दोहरा) हो सकता है
  • कोई वास्तविक हल नहीं भी हो सकता

---

10. द्विघात समीकरण के अनुप्रयोग

द्विघात समीकरणों का उपयोग किया जाता है:

• क्षेत्रफल व परिमाप संबंधी प्रश्नों में
• चाल, समय और दूरी की समस्याओं में
• आयु संबंधी प्रश्नों में
• संख्याओं के योग व गुणनफल में
• ज्यामितीय समस्याओं में

---

11. NCERT के महत्वपूर्ण बिंदु

• मानक रूप: ax² + bx + c = 0
• a ≠ 0 अनिवार्य है
• विविक्तक मूलों की प्रकृति बताता है
• द्विघात सूत्र सभी समीकरणों पर लागू होता है
• ग्राफ हमेशा परवलय होता है

---

12. महत्वपूर्ण सूत्र

• द्विघात सूत्र:

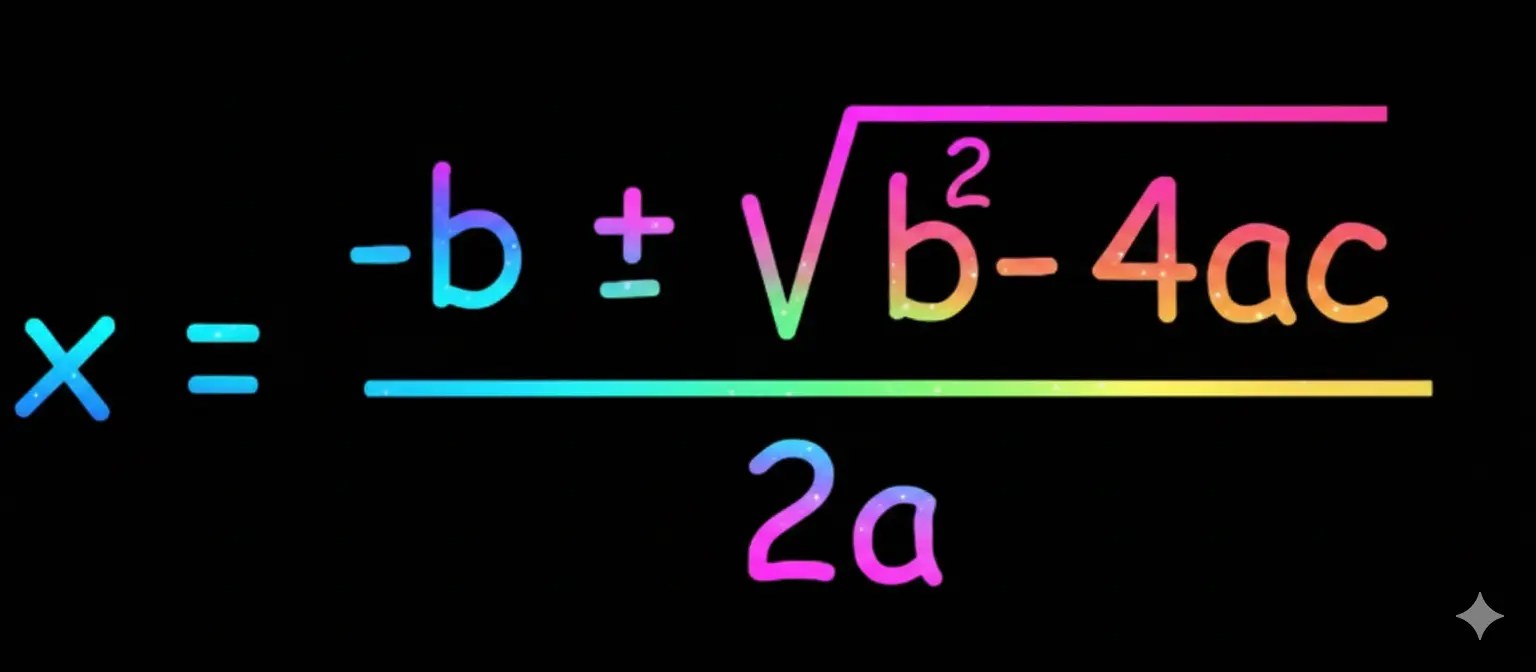
• विविक्तक:

D = b² – 4ac

---

13. सामान्य गलतियाँ

• a का मान शून्य मान लेना
• विविक्तक की गलत गणना
• चिह्नों (+/−) में गलती
• गलत गुणनखंड करना

---

14. त्वरित पुनरावृत्ति

• घात = 2
• अधिकतम मूल = 2
• विविक्तक से मूलों की प्रकृति ज्ञात
• परवलय ग्राफ
• बोर्ड परीक्षा के लिए अत्यंत महत्वपूर्ण अध्याय

---

15. Quick Revision One Shot Video : द्विघात समीकरण class 10