---

1. Introduction

• An equation involving one variable and having maximum power 2 is called a quadratic equation.
• Quadratic equations are widely used in algebra, geometry, physics, and daily life problems.
• The word quadratic comes from the Latin word “quadratus”, meaning square.

---

2. Standard Form of a Quadratic Equation

• A quadratic equation in variable x is written as:
  ax² + bx + c = 0
• Where:
  • a, b, c are real numbers
  • a ≠ 0
• If a = 0, the equation becomes linear, not quadratic.

---

3. Examples of Quadratic Equations

• x² + 5x + 6 = 0
• 2x² − 7x + 3 = 0
• x² − 4 = 0
• (x − 3)(x + 2) = 0

Not Quadratic Equations

• 3x + 5 = 0 (linear equation)
• x³ − 2x + 1 = 0 (degree 3)

---

4. Roots of a Quadratic Equation

• The solutions of a quadratic equation are called its roots.
• Roots are the values of x which satisfy the equation.
• A quadratic equation can have two roots (may be equal or different).

---

5. Methods of Solving Quadratic Equations (NCERT)

Quadratic equations can be solved by the following three methods:

(A) Factorisation Method

• Express the quadratic equation as a product of two linear factors.
• Set each factor equal to zero.
• Find the values of x.

Steps:

1. Write equation in standard form.
2. Factorise the middle term.
3. Equate each factor to zero.
4. Solve for x.

---

(B) Completing the Square Method

• Convert the equation into a perfect square.
• Useful when factorisation is difficult.

Steps:

1. Divide the equation by coefficient of x² (if not 1).
2. Move constant term to RHS.
3. Add square of half the coefficient of x on both sides.
4. Solve the resulting equation.

---

(C) Quadratic Formula Method

• Used when equation is not easily factorisable.
• The quadratic formula is:

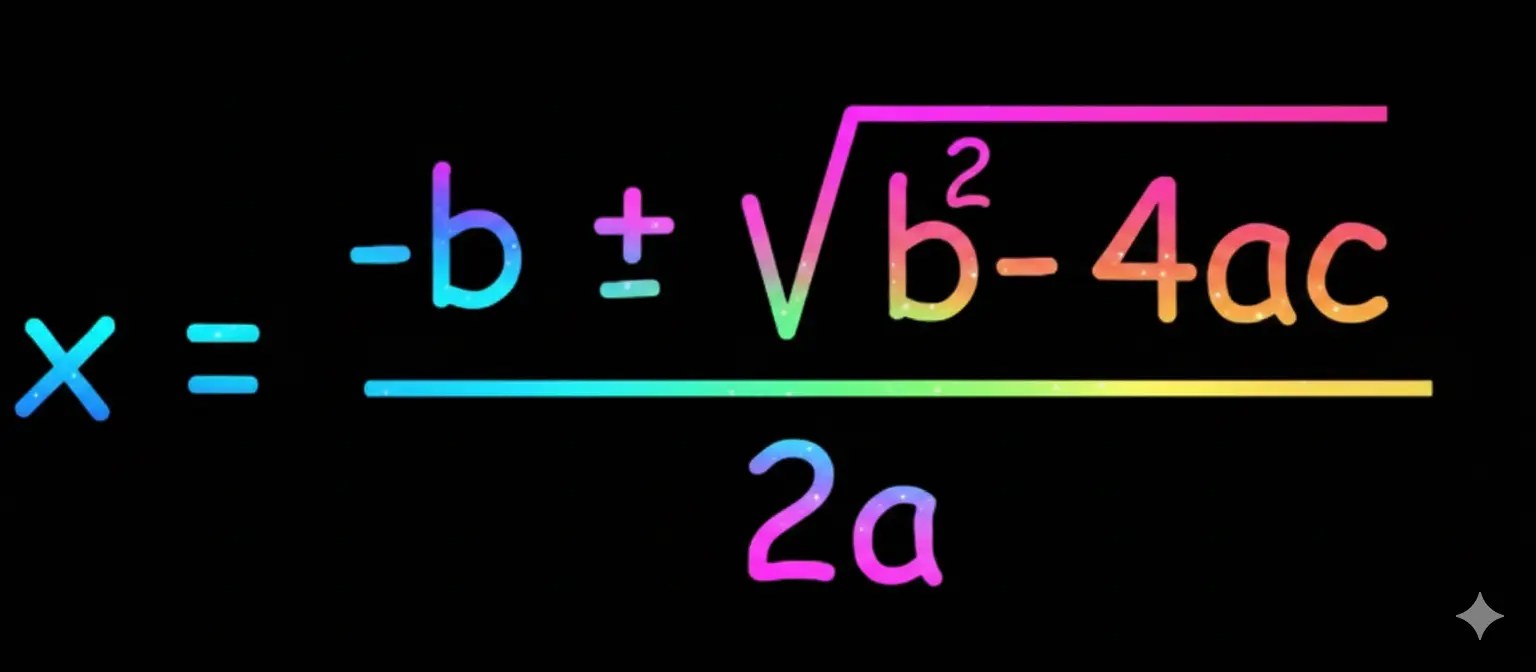
• Substitute values of a, b, c and simplify.

---

6. Discriminant

• The expression b² − 4ac is called the discriminant.
• Discriminant is denoted by D.

D = b² – 4ac

---

7. Nature of Roots Based on Discriminant

Value of D	Nature of Roots
D > 0	Two distinct real roots
D = 0	Two equal real roots
D < 0	No real roots

---

8. Geometrical Meaning of Quadratic Equation

• The graph of a quadratic equation represents a parabola.
• The roots are the points where the parabola cuts the x-axis.
• If the parabola:
  • Cuts x-axis at two points → two real roots
  • Touches x-axis at one point → equal roots
  • Does not touch x-axis → no real roots

---

9. Solution of a Quadratic Equation

• A quadratic equation may have:
  • Two real solutions
  • One real solution (repeated)
  • No real solution

---

10. Applications of Quadratic Equations

Quadratic equations are used to solve problems related to:

• Area and perimeter
• Speed, time, and distance
• Number problems
• Age problems
• Geometrical figures
• Product and sum of numbers

---

11. Important NCERT Points to Remember

• Standard form: ax² + bx + c = 0
• a ≠ 0 is compulsory
• Roots are obtained by factorisation, completing square, or quadratic formula
• Discriminant decides the nature of roots
• Quadratic formula is the most general method

---

12. Important Formulas

• Quadratic Formula:

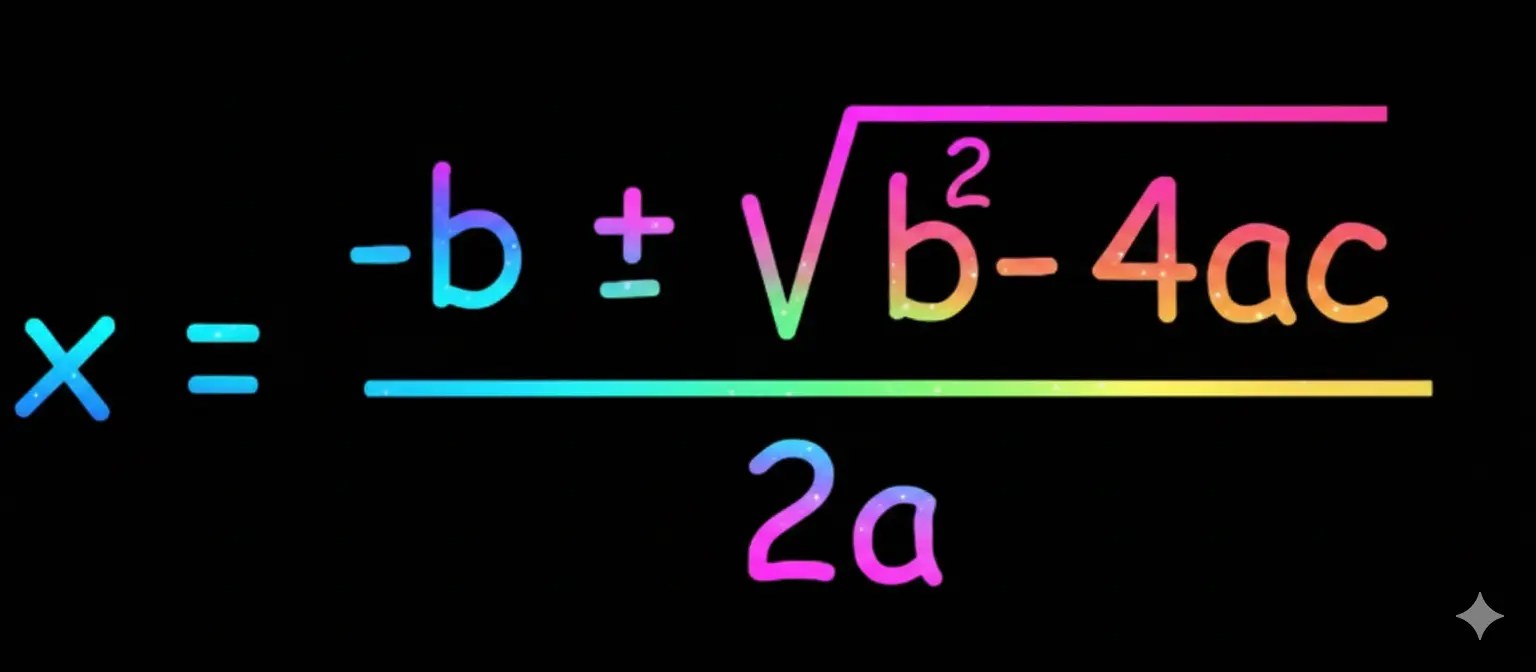
• Discriminant:
  D = b² – 4ac

---

13. Common Mistakes to Avoid

• Taking a = 0 in quadratic equation
• Wrong calculation of discriminant
• Sign errors in quadratic formula
• Incorrect factorisation

---

14. Quick Revision Summary

• Degree of quadratic equation = 2
• Maximum number of roots = 2
• Discriminant determines root nature
• Graph is always a parabola
• Quadratic formula works for all quadratic equations

---

15. Quick Revision One Shot Video : Quadratic Equations Class 10