Read In English

हम सीखेंगे :

1. परिचय
2. वैद्युत स्थैतिक स्थितिज ऊर्जा
3. वैद्युत स्थैतिक विभव
4. वैद्युत स्थैतिक बल संरक्षणी होते हैं
5. बिन्दु आवेश के कारण वैद्युत स्थैतिक विभव
6. विद्युत आवेशों के समूह के कारण किसी बिंदु पर विभव (Updating soon)

---

परिचय

• पिछले अध्याय में हमने बिन्दु आवेश तथा आवेश वितरण के कारण उत्पन्न विद्युत क्षेत्र (E) का अध्ययन किया।
• विद्युत क्षेत्र (E) एक सदिश राशि है जिसे विद्युत क्षेत्र तीव्रता कहते हैं।
• इस अध्याय में हम एक अदिश राशि (V) का अध्ययन करेंगे जिसे वैद्युत स्थैतिक विभव कहते हैं।
• वैद्युत स्थैतिक विभव (V):
  • किसी आवेशित पिण्ड के विद्युतीकरण की अवस्था को दर्शाता है।
  • यह निर्धारित करता है कि दो पिण्डों को संपर्क में रखने पर आवेश किस दिशा में प्रवाहित होगा।
  • आवेश सदैव उच्च विभव से निम्न विभव की ओर प्रवाहित होता है और दोनों का विभव समान होने पर प्रवाह रुक जाता है।
• कूलॉम के नियम से हम विद्युत क्षेत्र तीव्रता निकालते हैं, परंतु इस अध्याय में हम एक वैकल्पिक नियम गॉस का नियम पढ़ेंगे।
  • यह नियम विशेषकर साम्यिक आवेश वितरण के लिए विद्युत क्षेत्र निकालने में सहायक है।
  • इसके द्वारा जटिल वैद्युत स्थैतिक समस्याएँ सरल हो जाती हैं।

---

वैद्युत स्थैतिक स्थितिज ऊर्जा

• जैसे गुरुत्वाकर्षण क्षेत्र में स्थितिज ऊर्जा होती है, वैसे ही विद्युत क्षेत्र में किसी आवेश की वैद्युत स्थैतिक स्थितिज ऊर्जा होती है।
• मान लें मूलबिन्दु पर आवेश +Q रखा है और एक छोटा परीक्षण आवेश +q बिन्दु A से B तक लाया जाता है।
  • +q इतना छोटा है कि यह +Q की संरचना को प्रभावित नहीं करता।
  • एक बाहरी बल लगाया जाता है जो विद्युत बल को संतुलित करता है, ताकि संपूर्ण बल = 0 और +q बिना त्वरण के A से B तक चले।

• बाहरी बल द्वारा किया गया कार्य (Wext):
  • विद्युत बल द्वारा किये गये कार्य का ऋणात्मक होता है।
  • यह कार्य स्थितिज ऊर्जा के रूप में +q में संग्रहित हो जाता है।
• यदि B पर बाहरी बल हटा दिया जाए, तो विद्युत बल +q को दूर धकेल देगा और स्थितिज ऊर्जा → गतिज ऊर्जा में बदल जाएगी।
• हर बिन्दु पर आवेश q के पास कुछ न कुछ स्थितिज ऊर्जा होती है।
  • A से B ले जाने में किया गया कार्य = स्थितिज ऊर्जा का अंतर।
  • यह केवल प्रारम्भिक और अंतिम बिन्दुओं पर निर्भर करता है, पथ पर नहीं।

परिभाषा :

• दो बिन्दुओं A और B के बीच वैद्युत स्थैतिक स्थितिज ऊर्जा का अंतर = वह न्यूनतम कार्य जो बाहरी बल द्वारा परीक्षण आवेश q को (बिना त्वरण) A से B तक ले जाने में किया जाता है।
• वास्तविक स्थितिज ऊर्जा का मान महत्वहीन है, केवल अंतर महत्वपूर्ण है।
• परंपरा: अनन्त (∞) पर स्थितिज ऊर्जा = शून्य मानी जाती है।

अतः :

• किसी बिन्दु B पर आवेश q की वैद्युत स्थैतिक स्थितिज ऊर्जा = वह कार्य जो बाहरी बल (विद्युत बल के विपरीत और बराबर) द्वारा आवेश q को अनन्त से B तक लाने में किया जाता है।

---

वैद्युत स्थैतिक विभव

• परिभाषा (Potential Difference):
  • दो बिन्दुओं A और B के बीच वैद्युत स्थैतिक विभवांतर = वह कार्य जो एक इकाई धनात्मक परीक्षण आवेश को (बिना त्वरण) A से B ले जाने में किया जाता है।
  • यह कार्य विद्युत क्षेत्र के विरुद्ध किया जाता है।

• विशेषताएँ :
  • कार्य केवल प्रारम्भिक (A) और अंतिम (B) बिन्दुओं पर निर्भर करता है, पथ पर नहीं।
  • यदि बिन्दु A का विभव = VA और B का विभव = VB,
    U_B–U_A/q = W_AB/q = ΔV

• आयामी सूत्र (Dimensional Formula):
  [ML²T⁻³A⁻¹]
• SI इकाई :
  • Volt (V)
  • 1 volt = 1 joule / 1 coulomb = 1 J C⁻¹ = 1 N m C⁻¹
• परिभाषा (1 volt):
  • यदि 1 J कार्य कर एक 1 C धन आवेश को बिना त्वरण A से B तक ले जाया जाए, तो A और B के बीच विभवांतर = 1 volt।
• महत्वपूर्ण तथ्य :
  • भौतिक दृष्टि से केवल विभवांतर ही सार्थक है, किसी बिन्दु का वास्तविक विभव नहीं।
  • परिभाषा हेतु सामान्यतः अनन्त (∞) पर विभव = 0 माना जाता है।
• वैद्युत स्थैतिक विभव (at a point):
  • किसी बिन्दु पर वैद्युत स्थैतिक विभव = वह न्यूनतम कार्य जो एक इकाई धनात्मक आवेश को अनन्त से उस बिन्दु तक (बिना त्वरण) लाने में किया जाता है।
  • यह एक अदिश राशि (Scalar Quantity) है।
• 1 Volt परिभाषा (at a point):
  • यदि 1 J कार्य कर 1 C धनात्मक आवेश को अनन्त से उस बिन्दु तक लाया जाए, तो उस बिन्दु का विभव = 1 volt।

---

वैद्युत स्थैतिक बल संरक्षणी होते हैं

• कथन: वैद्युत स्थैतिक बल संरक्षणी (Conservative) होते हैं → किसी इकाई धनात्मक परीक्षण आवेश को किसी बंद पथ पर ले जाने में किया गया कार्य = शून्य।
• प्रमाण का विचार:
  • इकाई धनात्मक आवेश को A → B ले जाने में किया गया कार्य = WAB
  • उसी आवेश को B → A किसी अन्य पथ से ले जाने में किया गया कार्य = WBA
  • कुल कार्य (A → B → A):
    WAB+WBA=(VB–VA)+(VA–VB)=0WAB + WBA = (VB – VA) + (VA – VB) = 0
• निष्कर्ष:
  • बंद पथ पर आवेश ले जाने में कोई कार्य नहीं होता।
  • अतः वैद्युत क्षेत्र संरक्षणी होता है और वैद्युत स्थैतिक बल भी संरक्षणी बल हैं।
• गणितीय रूप:
  (बंद पथ पर विद्युत क्षेत्र का रेखा समाकलन सदैव शून्य होता है)

---

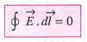
बिन्दु आवेश के कारण वैद्युत स्थैतिक विभव

बिन्दु आवेश के कारण विभव

• स्थिति: मूलबिन्दु O पर एक बिन्दु आवेश q रखा है। बिन्दु P पर विभव निकालना है जहाँ OP = r।
• परिभाषा: बिन्दु P पर वैद्युत स्थैतिक विभव = वह कार्य जो एक इकाई धनात्मक परीक्षण आवेश को अनन्त (∞) से P तक लाने में किया जाता है।
• विद्युत क्षेत्र:

  E = (1 / 4πɛ₀) · (q / x²)

  छोटे विस्थापन dx के लिए: dW = -E dx

• कुल कार्य (∞ → r):

  W = ∫_∞^r -(1 / 4πɛ₀) · (q / x²) dx

  विभव: V = q / (4πɛ₀ r)

• महत्वपूर्ण तथ्य:
  • q > 0 ⇒ V धनात्मक
  • q < 0 ⇒ V ऋणात्मक
  • r → ∞ पर V = 0
  • समान दूरी r पर विभव समान होता है → गोलीय सममिति
• परिवर्तन:

  V ∝ 1/r और E ∝ 1/r²

---

विद्युत आवेशों के समूह के कारण किसी बिंदु पर विभव (Updating soon)

जरूर पढ़ें :

1. स्थिर वैद्युत आवेश एवं क्षेत्र सम्पूर्ण नोट्स